Can you calculate Power accurately without a Power Meter?
Have you ever wondered if it’s possible to measure your power output accurately without a power meter?
Reading the forums it seems that people have experimented with this and found, not surprisingly, that in a controlled environment and for short runs it is possible to calculate power output that corresponds pretty closely to directly measured power. But out in the real world and as rides get longer and more varied the figures diverge markedly.
So I thought it would be interesting to review the methods used to calculate power and see where things can go wrong.
The total power required to move your bike forward is made up of 5 elements
- Power produced to overcome the rolling resistance of forward motion.
- Power produced to overcome wind resistance. (or air density).
- Power produced to overcome the pull of gravity (in the case of climbing hills).
- Power produced to accelerate from one speed to another.
- Power produced to overcome drive train losses through chains and gears.
The total power produced, P, is the sum of all five power components.
P= P(rolling resistance) + P(wind/air density) + P(gravity) + P(acceleration) + P(Drivetrain losses)
P (rolling resistance)
The power produced to overcome rolling resistance can be described by the formula:
P = Crr x N x v
P is the power required.
Crr is the coefficient of rolling resistance. This is a function of tyre type, rider weight, road surface and tyre pressure
N is the normal force of the bike and the athlete against gravity.
v is the velocity of the bike.
P(wind/air density)
The power produced to overcome wind resistance (drag) can be described by the formula:
P = 0.5 x ρ x v3 x Cd x A
P is the power required.
ρ is the air density.
v is the rider velocity, relative to the wind.
Cd is the drag coefficient.
A is the surface area of the rider facing the wind.
P(gravity)
The power produced to overcome the pull of gravity while riding up an incline can be described by the formula
P = m x g x sin(arctan(grade)) x v
P (the power required.
m (the mass of the rider and the bicycle.
g (the gravitational constant, 9.8.
grade (the slope of the hill.
P(acceleration)
The power produced to accelerate from one speed to another within a ride sampling window can be described by the formula
P = m x a x v
P (the power required.
m (the total mass of the rider and clothes/equipment and the bicycle.
a (the acceleration between your start speed and end speed.
P(Powertrain loses)
This is effectively a constant that depends on the condition and cleanliness of your chain and gears and can vary between 5% (for a new and clean drivetrain) and 15% (For a worn and dirty drivetrain)
Which variables cause inaccuracies in Power Calculation
Some of the values to calculate Power are constant, others are variable but easy to measure in real time, and finally, a few variables have a considerable impact on the results and are hard to measure.
They explain why accurately calculating Power in the real world is so challenging.
Values that are Pretty Much Constant
Crr (the coefficient of rolling resistance).
N (the normal force of the bike and the athlete against gravity).
ρ (the air density).
m (the total mass of the rider and clothes/equipment and the bicycle).
g (the gravitational constant, 9.8).
powertrain loses
Values that are Variable during the ride and Easy to Measure Accurately
V (the rider velocity).
m (the mass of the rider and the bicycle).
a (the acceleration between your starting speed and your ending speed).
Values that are Variable during the ride and Hard to Measure Accurately
Grade (is the slope of the hill).
V (the rider velocity, relative to the wind).
Cd (the drag coefficient or slipperiness of you and your bike *determined by what yo are wearing to a great extent).
A (the surface area of the rider facing the wind).
So there are 4 hard to Measure variables that we must use to calculate Total Power .
Hard to Measure Influential Variable one – Aerodynamic Drag
Cd and A are combined to create a scientific measurement called aerodynamic drag *written as CdA. The Cd part of this won’t change much as it is a function of your body shape and the clothes you are wearing.
The A part is the frontal area you present when riding and so could change dramatically and will have a huge impact on the power estimate. Think of the difference in power you need to ride at the same speed sitting up compared with on the drops
Here are a few figures from Bicycling Science" (Wilson, 2004). (It is unlikely these values included helmets).
Tops 0.632
Hoods 0.40
Drops 0.32
As I spend 99% of my time on the hoods this is not a variable for me, but you can see that if you spend a lot of the ride moving about on the bike it will have an impact on the power accuracy
Hard to Measure Influential Variable two – Velocity net of wind speed
Measuring velocity accurately is easy with a cheap sensor on the wheel hub, measuring Wind Speed and direction in real time is a little harder without specialized equipment.
Again it is obvious this has a big impact on power estimation. Imagine the difference in power required to ride into a 10Km/Hr Headwind compared with the same tailwind.
Garmin offers a premium app based on a web service called dark sky which they sample every 5 minutes and add to your ride data.
I am not really sure how accurate Darksky is, I assume it depends where you nearest measuring station is. As I write this I can look out of my window and see there is no wind yet Ddarksky is reporting 20 Mph ESE!
You could also try Wunderground which is similar to darksky but I would recommend you get a Hand Held anemometer. these are pretty cheap on Amazon and you might want to get one that also measures temperature, pressure and dew point as well.
Golden Cheetah lets you take a single Wind Speed and Direction reading and add it to your ride profile before estimating the power. If you leave the values blank GC assumes no wind (as does Strava). But if you put in wind speed (Km/Hr) and direction (Ideally measured at the center-of-mass height from a handheld anemometer), GC will calculate the wind direction throughout your route using the GPS plot which is pretty cool.
Strava ignore the effect of wind (their calculation assumes no wind)!
Velocomp produces a range of power meters that use Pitot tubes or their proprietary design “big mouth” wind port, these are reportedly VERY accurate.
Hard to Measure Influential Variable three – Grade
Grade is another variable that has a huge effect in your power estimate and is hard to measure. It relies on accurately measuring distance traveled (easy) and altitude (hard).
You can easily see that the power you need to climb a 5% grade is much less than that required to climb a 7% grade, but your Elevation estimate could easily cause an error of this magnitude.
Grade is vertical distance divided by horizontal distance expressed as a percentage (to make it easier to remember it is the rise over the run)
So Elevation is a key parameter and there are just two ways to measure it, neither of which is perfect.
From GPS coordinates
Elevation can be calculated using the distance of the device from the GPS satellites and for reasons too complicated for this blog are pretty inaccurate ranging from +/- 50 to 125 feet
From Barometric Pressure
This is the more accurate method as the device is measuring the difference in atmospheric pressure which decreases with altitude, for best results you need to calibrate the device at a known altitude.
Garmin says this about their devices
With the Auto Calibration feature turned on, the altimeter accuracy can range from +/- 50 to 125 feet (same as GPS elevation). With a strong GPS connection with WAAS, (a system of satellites and ground stations that provide GPS signal corrections, giving you even better position accuracy) it's possible to obtain an accuracy of +/- 25 to 50 feet.
When manually calibrating (Auto Calibration off) to a known elevation it is approximately +/- 10 feet for the first 15 minutes. If needing accurate elevation, it is recommended to calibrate the altimeter hourly to maintain its accuracy because of possible pressure changes.
Strava have a database of elevation values created using data uploaded by the community
By collecting the barometric altimeter measurements from any activity uploaded to Strava in the past, they have been able to build a global elevation database. Not only is this basemap more accurate than previous elevation methods, but it will result in more consistent calculations between devices, both with or without a barometric altimeter.
In conclusion, there are four key variables that affect the accuracy of calculated power
- Frontal Area
- Windspeed
- Grade
- Drivetrain Condition
By optimizing measurement methods and minimizing the variability of these values, and bearing in mind that even direct measurement devices are not 100% accurate (especially left only devices) I think it is perfectly viable for amateurs and enthusiasts to train using calculated power.
If you want to experiment with calculating cycling power then Golden Cheetah is a good place to start as it gives you a lot of control over the parameters and also has a useful tool called Aerolab which lets you estimate your aero drag values.
Velocomp produce a range of very low cost (USD $199) power meters that use the concepts discussed above to produce results comparable with direct measurement power meters and power pedals
I will be updating this post on a regular basis so please keep checking back and feel free to comment using the form below
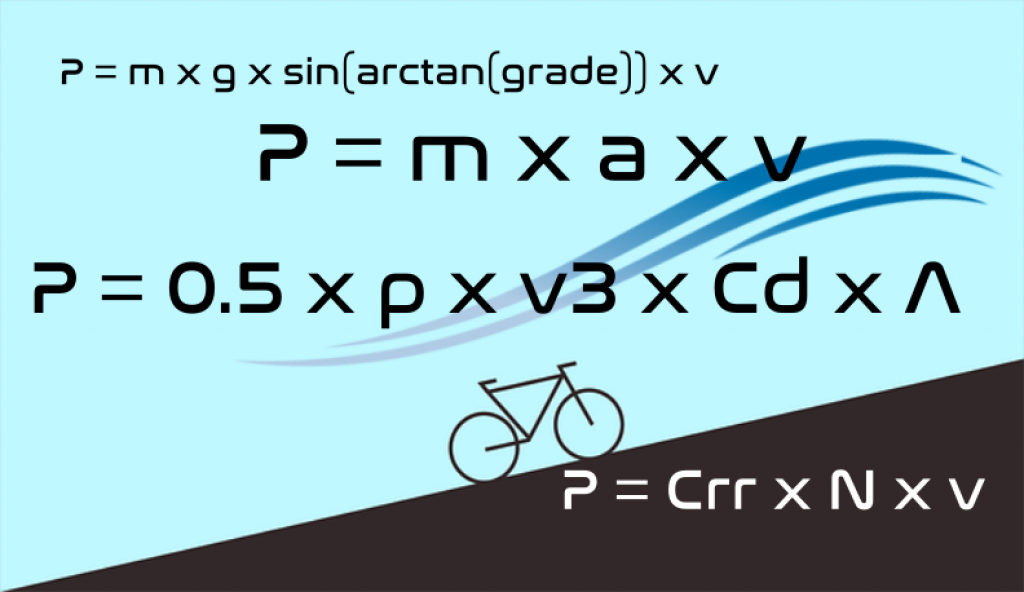



Leave A Comment
You must be logged in to post a comment.